Diffusion (1) Model Background

What is Diffusion Model

Data 에 Noise 를 조금씩 더해가거나 noise 로부터 조금씩 복원해가는 과정으로 Data 를 생성하는 모델

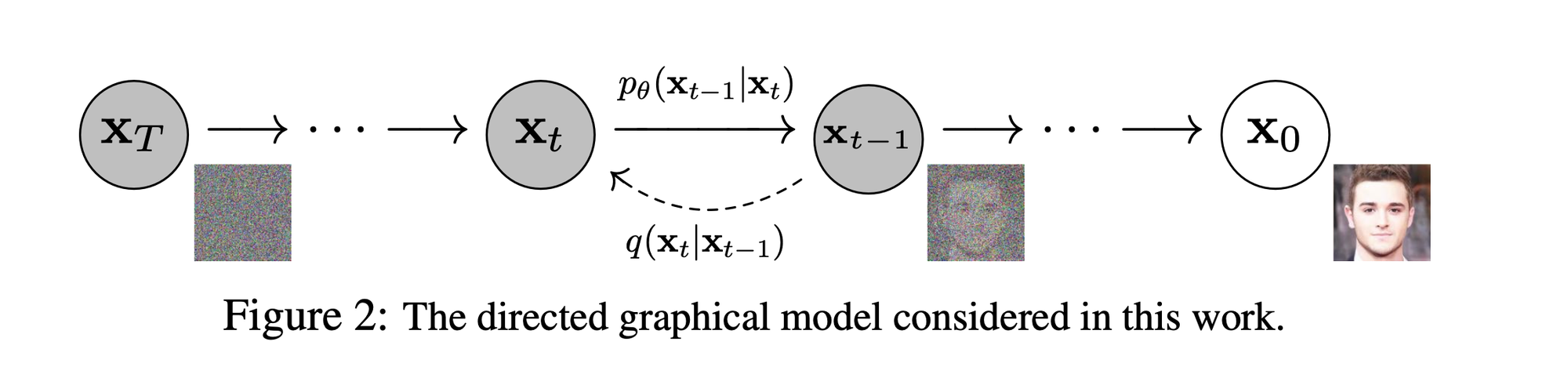
위 그림에서 는 실제 데이터, 는 최종 Noise, 중간의 는 Data 에 Noise 가 더해진 상태의 Latent variable

1. Forward Process
   → 데이터에 노이즈를 더해가는 과정
2. Reverse(Backward) Process
   → 반대로 노이즈를 제거하면서 추정해가는 과정

→ 이 Reverse Process 를 활용해서 Random noise 로부터 우리가 원하는 image, text, graph 등을 생성하는 모델을 만들어내는 것

작동 원리

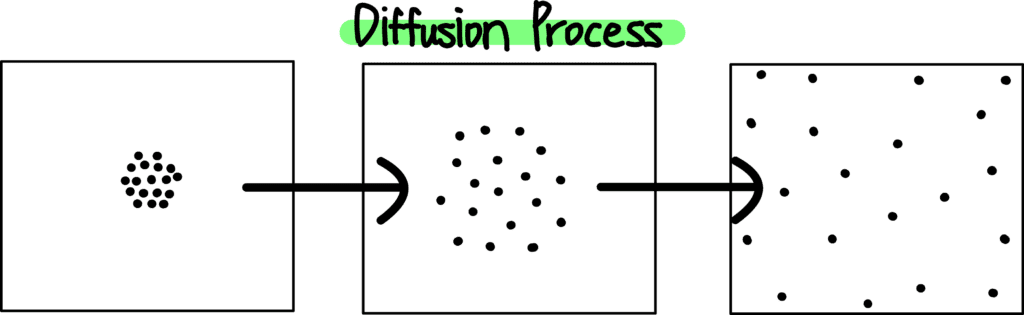
일부 공간에 모여 있던 분자들이 Diffusion Process 를 거쳐 전 공간에 일정하게 분포하는 현상을 표현

→ 분자 하나의 움직임을 관찰하면 다음과 같이 움직인다
분자의 움직임이 Gaussian Distribution 을 따르는 이유? 분자의 움직임을 추정하기 위한 다양한 확률 분포를 고려할 수 있으나 Gaussian distribution 이 가장 추정하기 쉽기 떄문

정규분포를 따른다

그렇다면 한 이미지의 전체 픽셀이 정규분포를 따른다는 것은 어떤 이미지의 형태를 보이는 것이 아닌 노이즈의 형태여야하는 것? 그렇다면 노이즈처럼 보이는 이미지가 정규분포를 따르는 상태인 것?

Forward Diffusion Process

→ Noise 를 더할 때, Variance Scheduler 를 사용해서 scaling 을 한 후에 더한다 (Why? 단순히 노이즈만 추가하게 되면 variance 가 발산할 수 있기 때문에 Scaling 을 거치는 것, 이 과정을 통해 Variance 가 일정수준으로 유지)

→ 데이터가 원본 이미지와 유사할 때( Forward 초기)에는 이 값을 매우 작게, Gaussian Distribution 에 점점 가까워질수록 (Forward 말기) 이 값을 크게 설정 ( 까지 lInear 하게 증가)

이렇다고 얘기하는 데 정확하게 이 식을 이해하지는 못함 (→ 한 step씩 학습을 하면 메모리와 resource가 너무 많이 든다. 그러나 이런식으로 한번에  를 만들고 나면, 여기서 loss를 구한 다음에 t에 대한 expectation을 구하는 식으로 학습이 가능하다 (어차피 stochastic gradient를 사용하기 때문에 이런식으로 학습해도 무방) → 해당 증명은 Reference#2 에서 증명하고 있으니 참고.

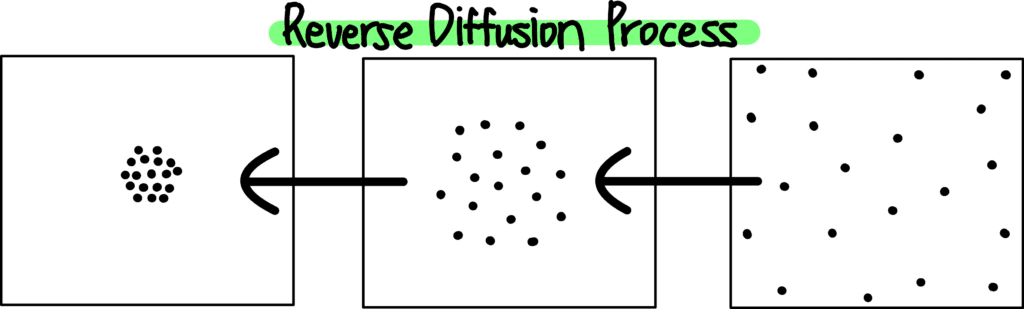
Reverse Diffusion Process

시간 t 마다 이미지 픽셀 값에 어떤 noise 가 첨가되었는지 그 값을 계산할 수 있다면 Noise 이미지 로부터 원본 이미지 로 되돌리는 것이 가능 → 이 말은 곧 어떤 Noise 를 집어넣으면 이 과정을 거쳐서 이미지가 생성된다는 것과 동일하다.
→ 하지만 이 값을 예측하는 것이 어렵기 때문에 를 활용해서 이 값을 추정한다 (Approximate)
이 추정의 형태는 Gaussian Transition 을 활용한 Markov chain 의 형태를 가진다.

위 식에서 각 단계의 정규 분포의 평균 와 표준편차 는 학습되어야하는 Parameter (어떤 분포를 포현할 때 Gaussian 들의 합성으로 표현하는데 이 때, 각 Gaussian 의 평균과 표준편차를 알아야하니까?)
그리고 위 식의 시작 지점인 Noise() 의 분포는 다음과 같이 가장 간단한 형태의 표준정규분포로 정의

Objective Function

Parameter 를 추정하기 위해서 Diffusion model 은 어떻게 학습하는가?

목표 : 실제 데이터의 분포인 를 찾아내는 것
( = 결국 주어진 noise에 대해 어떻게 noise를 점진적으로 걷어낼 것이냐의 문제 )
→ 이 분포(생성된 이미지)의 Log Likelihood 를 최대화(= Maximize Negative Log Likelihood) 하는 것이 우리의 목적

Reference#2 에서 해당 공식의 증명과정을 설명하고 있으니 참고하면 좋을 것 같다.
→ 결론적으로는 우리가 diffusion model 을 학습할 때의 Training loss 가 정규 분포 사이의 KL Divergence 형태로 쉽게 계산될 수 있다는 것을 설명하는 내용

특이한 점은 forward process의 posterior와 reverse process를 KL Divergence를 통해 직접 비교한다는 것이다. 생각해보면 forward process에 대한 정보를 가지고 있고 forward process의 posterior는 reverse process와 연관이 깊은 형태이기 때문에 tractable하다.
→ 라고 Reference#3 에서 설명하고 있는데 tractable 하다는 것이 둘이 비슷하기 때문에 연관성을 찾아 풀어낼 수 있다 이런느낌으로 생각하면 될지 잘 모르겠다…

---

Reference

#1 https://ffighting.net/deep-learning-paper-review/diffusion-model/diffusion-model-basic/
#2 https://jang-inspiration.com/ddpm-1
#3 https://jang-inspiration.com/ddpm-2
#5 Latex

Link

---

“이 글은 Obsidian 에서 작성되어 업로드 되었습니다”